등각속도로 도는 입력이 있다고 합시다
즉 일정한 속도로 도는겁니다
여기에 맞물려도는 기어가 있고 그것을 출력이라고 하고요.
출력에서 관찰하면 일정한속도로 돌겠지요(@@@)
수학적으로 그냥 접근을 해 보았습니다.
등각속도 구간이 아닌 가속도 구간은 없을까
즉 정말로 1.0000000000000:1(또는 다른 고정값)의 비가 언제나 유지되는 수학적 기어구조가 있을까?
웜기어의 구조에서는 수학적으로 직선성이 될거라고 생각이 듭니다만 스퍼기어에서는 어떤(구슬이 내려오는 미끄럼틀 곡선처럼)곡선이 있지않을까 하는 생각이 들었습니다.
약 50 시간 생각거리 입니다. ㅎㅎ
-
28일 1시10분 추가
이곡선을 치형곡선 이라고 하네요(검색)
오일러의 이름이 나옵니다
이제 다음 단계는 실제가공에서 이곡선을 얼마나 잘만들수 있느냐로 넘어갑니다
Ps.구슬이 내려오는(가장빨리) 곡선이 사이클로이드 이며 치형곡선도 사이크로이드 랍니다
-
28일 23시59분 추가
잘 만드냐의 단계로 가기전에 생각할것이 생겼습니다.
제목의 내용을 한번 곱십어 봤습니다.
평기어평기어가 치형곡선으로 되었다고 해도
두기어가 빈틈없이 맞는것 뿐인지(치형곡선의 의미는 똑 맞는다는 겁니다), 아니면 일정한 각속도까지 갖는지 의문이 들었습니다
풀어쓰면 이런 의미 입니다
평기어의 입력을 0.000001도씩 한번씩 조금 쉬면서 돌린다고 봅시다
출력도 0.000001도씩 돌아갈까요?
그렇다면 직선성이 있다고 하는거고요
직관으로는 아닐것 같아서요
한개의 피치 주기로 보면 직선성이 있지만
아무리 치형곡선이라도 내 직관은 아닌걱 같은데,,,
치형곡선의 수학표현을 봐야하겠습니다
-
하모닉드라이브의 주기오차를 생각하다가 이런 의문이 든겁니다
-
3월2일 2시40분 추가
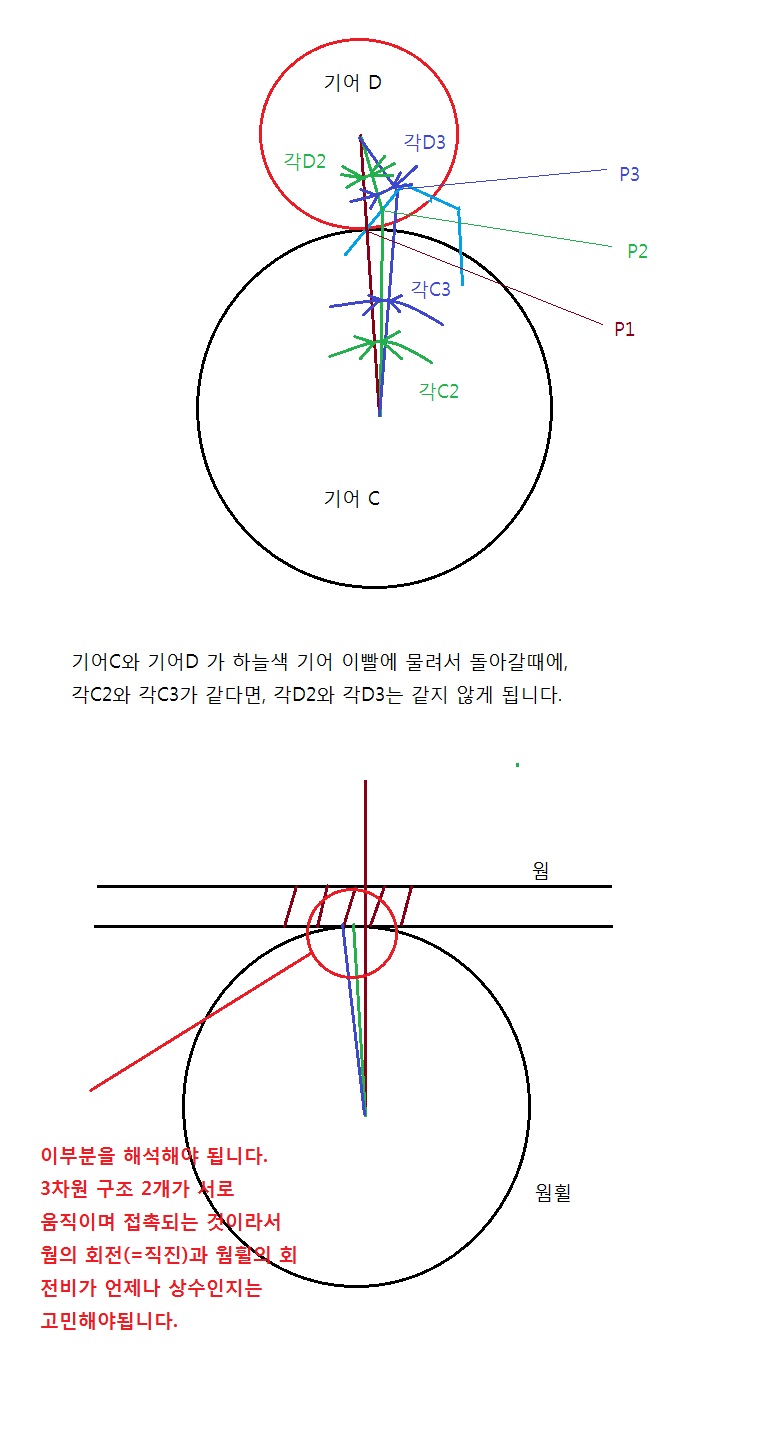
곰곰히 이리저리 등등등 자가고문을 해보니 평기어에서는 직선성을 가질수 없었습니다
평기어가 ( 피치원이 아닌곳에서의 접촉이 있다면 )임의의(=모든)각C 에대해서 각C/각D는 같지않습니다(=상수가 아닙니다=주기오차는 태생부터 있는겁니다)
끝=왜 적도의에 웜기어를 그동안 썼는지 알았습니다
-
3월2일 13시39분 추가
그림을 추가 합니다.
이제부터는 웜휠에서 수학적으로 주기오차가 빌생하는지 생각시작입니다.

-
3월2일 14시23분 추가
평기어의 주기오차 최소값(실제적으로 기어를 설계값으로 가장 정밀하게 만들었을때)을 계산할수 있겠네요.
p3 지나서 최정점에서 맞물이는 위치를 알면 그 위치가 최대로 오차가 벌어지는 지점 이니까요.
p1-p2-p3- 의 곡선 에서 최고로 올라간 지점이 각c/각d 의 값이 제일 벌어지는 곳이니까요.
(최고로 올라간 곳인지, 아니면 최고에서 유지 하다가 내려오기 시작할 때 까지의 중간인지는 좀더 생각-아마도 유지하는 포인트는 없을듯-점정찍자마자 내려올듯)
평기어서의 주기오차 커브가 상하대칭이 아네네요.......p1-p2-p3-로 이어지는 커브(각) 와 p1-p2"-p3" (" 은 왼쪽으로 이어진 곡선이라고 치면) 로 이어지는 각은 대칭이 아니니까요요.
-
3월4일 0시56분 추가
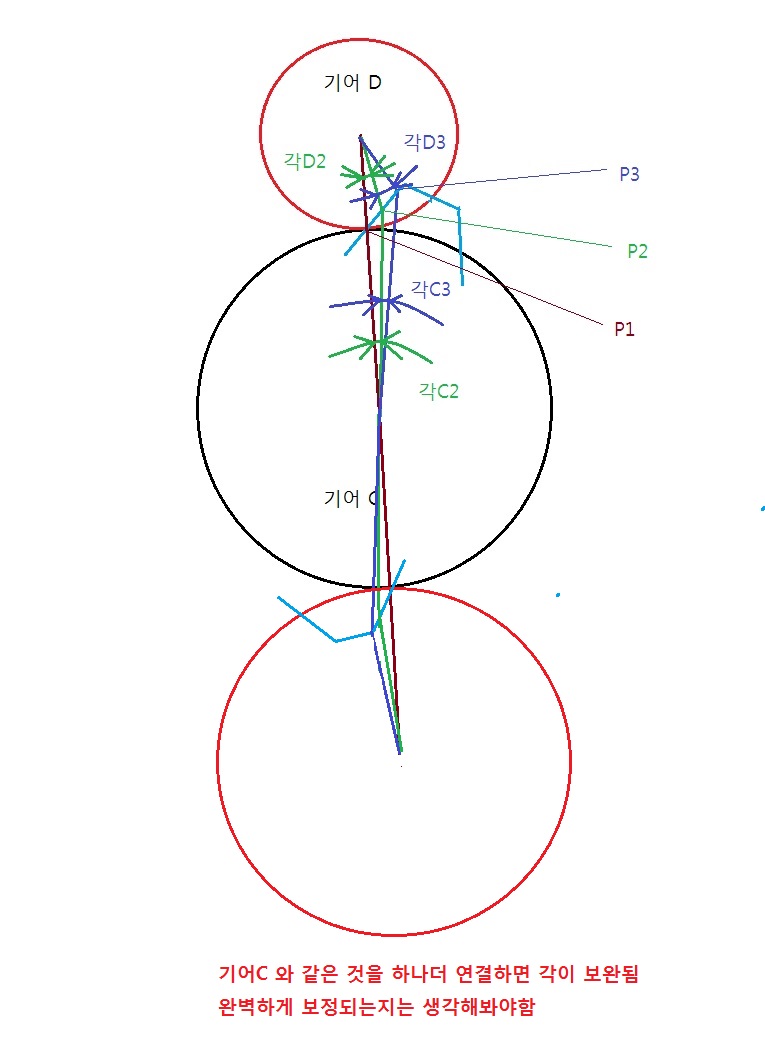
위의 평기어에서의 주기오차를 보정할 방안이 있기는 있는것 같습니다. 평기어를 하나 더달면 오차가 확 줄어들지만,
수학적으로 완전할지는 더 생각해봐야 합니다.